그래프 순회 문제란 특정 정점에서 시작하여 나머지 모든 정점을 방문하는 문제를 그래프 문제라고 한다.
그래프 순회 문제는 그래프에서 특정 정점을 찾기 위한 용도로 사용할 수 있기 때문에 그래프 탐색 문제(graph search problem)라고 부르기도 한다. 오늘 알아볼 것은 여러 그래프 탐색 알고리즘 중 하나인 너비 우선 탐색에 대한 내용이다.
너비 우선 탐색
너비 우선 탐색(BFS)은 시작 정점을 경계에 추가하는 것으로 시작한다.
(1)의 검정 동그라미가 시작정점이라고 했을 때 퍼져나가는 모습을 표현했다.
그림 예
(1)

(2)
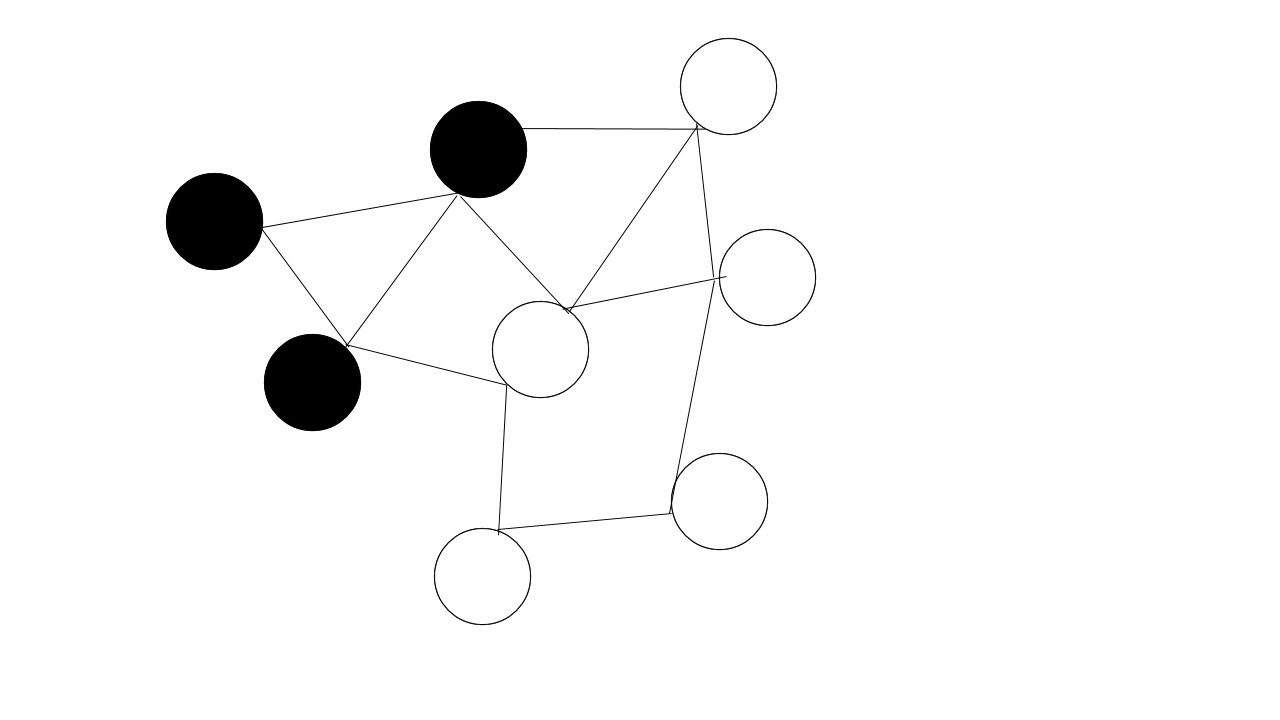
(3)

(4)

(5)

즉 이렇게 시작 지점에서 경계에 인접한 정점을 반복적으로 탐색하는 방법을 가진다.
이렇게 되면 전체 그래프를 순회할 수 있게 된다.
구현
#include <string>
#include <vector>
#include <iostream>
#include <set>
#include <map>
#include <queue>
using namespace std;
template<typename T>
struct Edge {
unsigned src;
unsigned dst;
T weight;
};
template<typename T>
class Graph {
public:
// N개의 정점으로 구성된 그래프
Graph(unsigned N) : V(N) {}
// 그래프의 정점 개수 반환
auto vertices() const { return V; }
// 전체 에지 리스트 반환
auto& edges() const { return edge_list; }
// 정점 v에서 나가는 모든 에지를 반환
auto edges(unsigned V) const {
vector<Edge<T>> edges_from_v;
for (auto& e : edge_list) {
if (e.src == V)
edges_from_v.emplace_back(e);
}
return edges_from_v;
}
void add_edge(Edge<T>&& e) {
// 에지 양 끝 정점 ID가 유효한지 검사
if (e.src >= 1 && e.src <= V && e.dst >= 1 && e.dst <= V)
edge_list.emplace_back(e);
else
cerr << "에러 : 유효 범위를 벗어난 정점!" << endl;
}
template <typename U>
friend ostream& operator<< (ostream& os, const Graph<U>& G);
private:
unsigned V;
vector<Edge<T>> edge_list;
};
template <typename U>
ostream& operator<< (ostream& os, const Graph<U>& G) {
for (unsigned i = 1; i < G.vertices(); i++) {
os << i << " :\t";
auto edges = G.edges(i);
for (auto& e : edges)
os << "{" << e.dst << ": " << e.weight << "}, ";
os << endl;
}
return os;
}
template<typename T>
auto create_reference_graph() {
Graph<T> G(9);
map<unsigned, vector<pair<unsigned, T>>> edge_map;
edge_map[1] = { { 2, 0 }, { 5, 0 } };
edge_map[2] = { { 1, 0 }, { 5, 0 }, { 4, 0 } };
edge_map[3] = { { 4, 0 }, { 7, 0 } };
edge_map[4] = { { 2, 0 }, { 3, 0 }, { 5, 0 }, { 6, 0 }, { 8, 0 } };
edge_map[5] = { { 1, 0 }, { 2, 0 }, { 4, 0 }, { 8, 0 } };
edge_map[6] = { { 4, 0 }, { 7, 0 }, { 8, 0 } };
edge_map[7] = { { 3, 0 }, { 6, 0 } };
edge_map[8] = { { 4, 0 }, { 5, 0 }, { 6, 0 } };
for (auto& i : edge_map) {
for (auto& j : i.second) {
G.add_edge(Edge<T>{ i.first, j.first, j.second });
}
}
return G;
}
template<typename T>
auto breadth_first_search(const Graph<T>& G, unsigned start) {
queue<unsigned> queue;
set<unsigned> visited; // 방문한 정점
vector<unsigned> visit_order; // 방문 순서
queue.push(start);
while (!queue.empty()) {
auto current_vertex = queue.front();
queue.pop();
// 현재 정점을 이전에 방문하지 않았다면
if (visited.find(current_vertex) == visited.end()) {
visited.insert(current_vertex);
visit_order.push_back(current_vertex);
for (auto& e : G.edges(current_vertex)) {
// 인접한 정점 중에서 방문하지 않은 정점이 있다면 큐에 추가
if (visited.find(e.dst) == visited.end()) {
queue.push(e.dst);
}
}
}
}
return visit_order;
}
int main() {
using T = unsigned;
// 그래프 객체 생성
auto G = create_reference_graph<T>();
cout << "[입력 그래프]" << endl;
cout << G << endl;
cout << "[BFS 방문 순서]" << endl;
auto bfs_visit_order = breadth_first_search(G, 1);
for (auto v : bfs_visit_order)
cout << v << endl;
return 0;
}
BFS의 시간 복잡도는 O(V + E)가 된다. 여기서 V는 정점의 개수이고, E는 에지의 개수를 의미한다.
알기 위해서 쉬운 코드로 작성해보았다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
bool visited[9];
vector<pair<int, int>> graph[9];
void bfs(int start) {
queue<int> q;
q.push(start);
visited[start] = true;
while (!q.empty()) {
int x = q.front();
q.pop();
cout << x << endl;
for (int i = 0; i < graph[x].size(); i++) {
int y = graph[x][i].first;
if (!visited[y]) {
q.push(y);
visited[y] = true;
}
}
}
}
int main(void)
{
graph[1].push_back({ 2, 0 });
graph[1].push_back({ 5, 0 });
graph[2].push_back({ 1, 0 });
graph[2].push_back({ 5, 0 });
graph[2].push_back({ 4, 0 });
graph[3].push_back({ 4, 0 });
graph[3].push_back({ 7, 0 });
graph[4].push_back({ 2, 0 });
graph[4].push_back({ 3, 0 });
graph[4].push_back({ 5, 0 });
graph[4].push_back({ 6, 0 });
graph[4].push_back({ 8, 0 });
graph[5].push_back({ 1, 0 });
graph[5].push_back({ 2, 0 });
graph[5].push_back({ 4, 0 });
graph[5].push_back({ 8, 0 });
graph[6].push_back({ 4, 0 });
graph[6].push_back({ 7, 0 });
graph[6].push_back({ 8, 0 });
graph[7].push_back({ 3, 0 });
graph[7].push_back({ 6, 0 });
graph[8].push_back({ 4, 0 });
graph[8].push_back({ 5, 0 });
graph[8].push_back({ 6, 0 });
// 1번부터 탐색 시작
bfs(1);
}

위 코드를 그림으로 표현하면 이렇게 된다.
BFS는 큐를 사용하여 나타낸다. 그리고 위 글에서 가중치는 0으로 잡고 만들었다.
출처 : 코딩 테스트를 위한 자료 구조와 알고리즘 with C++
++2024.03.21 Python 코드 추가
from collections import deque
visit = [False] * 9
def bfs(graph, start, visit):
queue = deque([start])
visit[start] = True
while queue:
v = queue.popleft()
print(v, end = " ")
for i in graph[v]:
if not visit[i]:
queue.append(i)
visit[i] = True
graph = [
[],
[2, 5], # 1
[1, 4, 5], # 2
[4, 7], # 3
[2, 3, 5, 6, 8], # 4
[1, 2, 4, 8], # 5
[4, 7, 8], # 6
[3, 6], # 7
[4, 5, 6] # 8
]
bfs(graph, 1, visit)'컴퓨터 과학 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 동적계획법(Dynamic Programming) (0) | 2024.08.09 |
|---|---|
| [알고리즘] 다익스트라 알고리즘(Dijkstra) (0) | 2024.03.18 |
| [알고리즘] 깊이 우선 탐색(DFS, Depth-First Search) (0) | 2024.03.13 |
| [알고리즘] 탐욕(그리디) 알고리즘(Greedy algorithm) (0) | 2024.02.08 |
| [알고리즘] 소수(Prime Number) 구하기 (1) | 2024.01.29 |