프림 알고리즘(Prim's Algorithm)은 그래프에서 최소 신장 트리를 찾는 그리디 알고리즘입니다. 최소 신장 트리란, 모든 노드가 연결되면서 그 가중치 합이 최소가 되는 트리를 의미합니다. 이 알고리즘은 네트워크 설계, 전선 연결 등에서 활용될 수 있습니다.
알고리즘 개요
프림 알고리즘은 그래프에서 시작 노드를 선택한 후, 가장 작은 가중치를 가진 간선을 하나씩 선택해 나가는 방식입니다. 즉, 트리를 단계적으로 확장해 나가는 그리디한 접근을 사용합니다.
프림 알고리즘 과정
- 시작 노드 선택: 임의의 노드를 시작점으로 선택합니다.
- 트리 확장: 트리에 포함되지 않은 노드 중에서, 트리에 가장 작은 가중치로 연결될 수 있는 간선을 선택하여 해당 노드를 트리에 포함시킵니다.
- 반복: 트리에 속하지 않은 모든 노드가 트리에 포함될 때까지 과정을 반복합니다.
알고리즘 설명
- 모든 노드를 방문하지 않았다고 가정하고, 하나의 시작 노드를 선택합니다.
- 선택된 노드와 연결된 간선 중에서 가장 작은 가중치를 가지는 간선을 선택하여 새로운 노드를 추가합니다.
- 새로운 노드와 기존 트리의 노드를 연결하는 간선 중에서 가장 작은 가중치를 선택하여 노드를 추가합니다.
- 이 과정을 반복하여 모든 노드를 연결합니다.
그림 설명
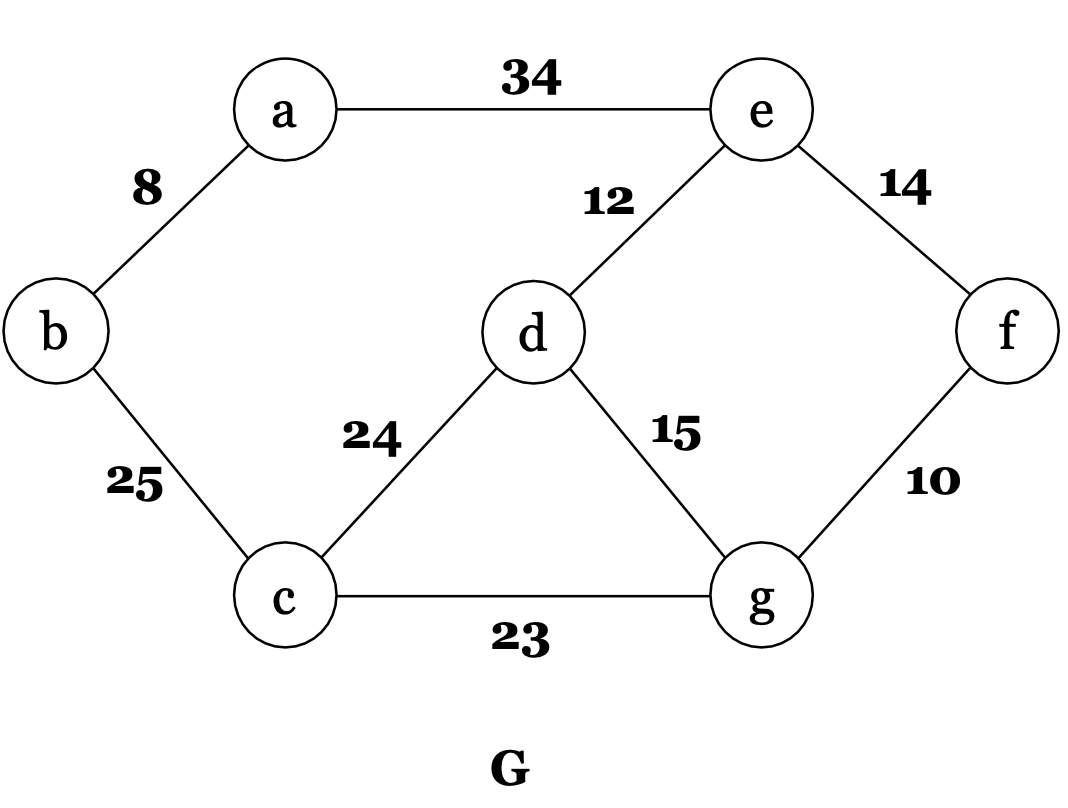
그래프 G가 있습니다!




각 노드에서 가장 작은 가중치를 따라가는 알고리즘을 사용하고 있습니다.
코드 예시
import heapq
def prim(graph, start):
mst = [] # 최소 신장 트리에 포함된 간선
visited = set([start]) # 방문한 노드
edges = [(cost, start, to) for to, cost in graph[start]] # 시작 노드의 간선 리스트
heapq.heapify(edges) # 최소 힙으로 변환
while edges:
cost, frm, to = heapq.heappop(edges) # 가장 작은 가중치를 가진 간선 선택
if to not in visited:
visited.add(to) # 방문 처리
mst.append((frm, to, cost)) # 최소 신장 트리에 간선 추가
for next_to, next_cost in graph[to]: # 새로 추가된 노드의 인접 노드 탐색
if next_to not in visited:
heapq.heappush(edges, (next_cost, to, next_to))
return mst
# 그래프 예시 (인접 리스트)
graph = {
'A': [('B', 1), ('C', 5), ('D', 3)],
'B': [('A', 1), ('D', 4), ('E', 2)],
'C': [('A', 5), ('D', 3)],
'D': [('A', 3), ('B', 4), ('C', 3), ('E', 4)],
'E': [('B', 2), ('D', 4)]
}
mst = prim(graph, 'A')
print(mst)프림 알고리즘을 사용한 예시 입니다. 위 사진과 다르게 다른 그래프를 사용하고 있지만 똑같은 알고리즘을 사용하고 있습니다.
'컴퓨터 과학 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 분할정복(Divide and Conquer) (1) | 2024.10.07 |
|---|---|
| [알고리즘] Greedy Algorithm - Interval Scheduling (0) | 2024.09.23 |
| [알고리즘] 비트마스크(BitMask) (0) | 2024.09.20 |
| [알고리즘] 투 포인터(Two Pointer) (3) | 2024.09.02 |
| [알고리즘] 이분 탐색(Binary Search) (0) | 2024.08.24 |