*문제 출처는 백준에 있습니다.
문제 제목: 친구 네트워크 / 4195번 (골드 2단계)
문제 사이트: https://www.acmicpc.net/problem/4195
문제 설명
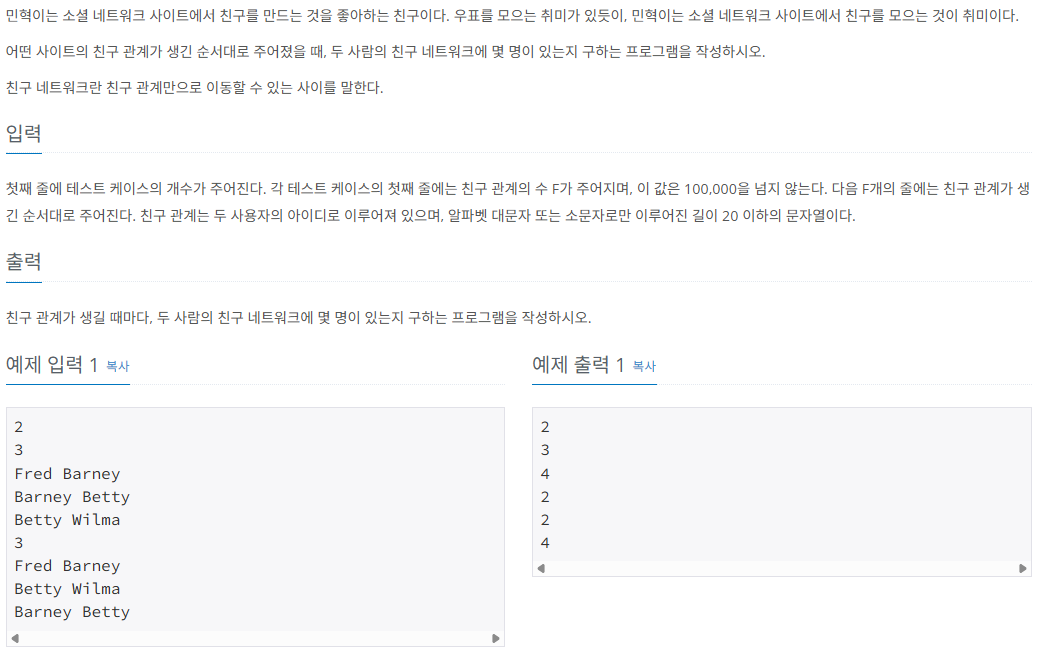
나의 풀이
# 특정 노드의 루트(대표자)를 찾는 함수
def find(x, parent):
# 부모가 자기 자신이 아니라면 (즉, 루트가 아니라면)
if parent[x] != x:
# 경로 압축: 부모를 루트로 바로 연결
parent[x] = find(parent[x], parent)
return parent[x]
# 두 노드를 하나의 집합으로 합치는 함수
def union(x, y, parent, size):
# 각각의 루트 노드(대표자)를 찾는다
x_root = find(x, parent)
y_root = find(y, parent)
# 두 사람이 같은 네트워크가 아니라면 합친다
if x_root != y_root:
# y_root를 x_root 밑으로 붙임
parent[y_root] = x_root
# x_root 집합의 크기를 업데이트
size[x_root] += size[y_root]
# 합쳐진 네트워크의 전체 인원 수를 반환
return size[x_root]
def main():
t = int(input()) # 테스트 케이스 개수 입력
for _ in range(t):
f = int(input()) # 친구 관계 수
parent = dict() # 각 사람의 부모(대표자)를 저장하는 딕셔너리
size = dict() # 각 대표자가 가진 네트워크 크기 저장
for _ in range(f):
a, b = input().split() # 친구 관계 입력
# 아직 등장하지 않은 사람은 초기화
if a not in parent:
parent[a] = a # 자기 자신을 부모로 설정
size[a] = 1 # 네트워크 크기 1로 시작
if b not in parent:
parent[b] = b
size[b] = 1
# 친구 관계를 합치고 네트워크 크기를 출력
print(union(a, b, parent, size))
main()
※ 알아야 할 것
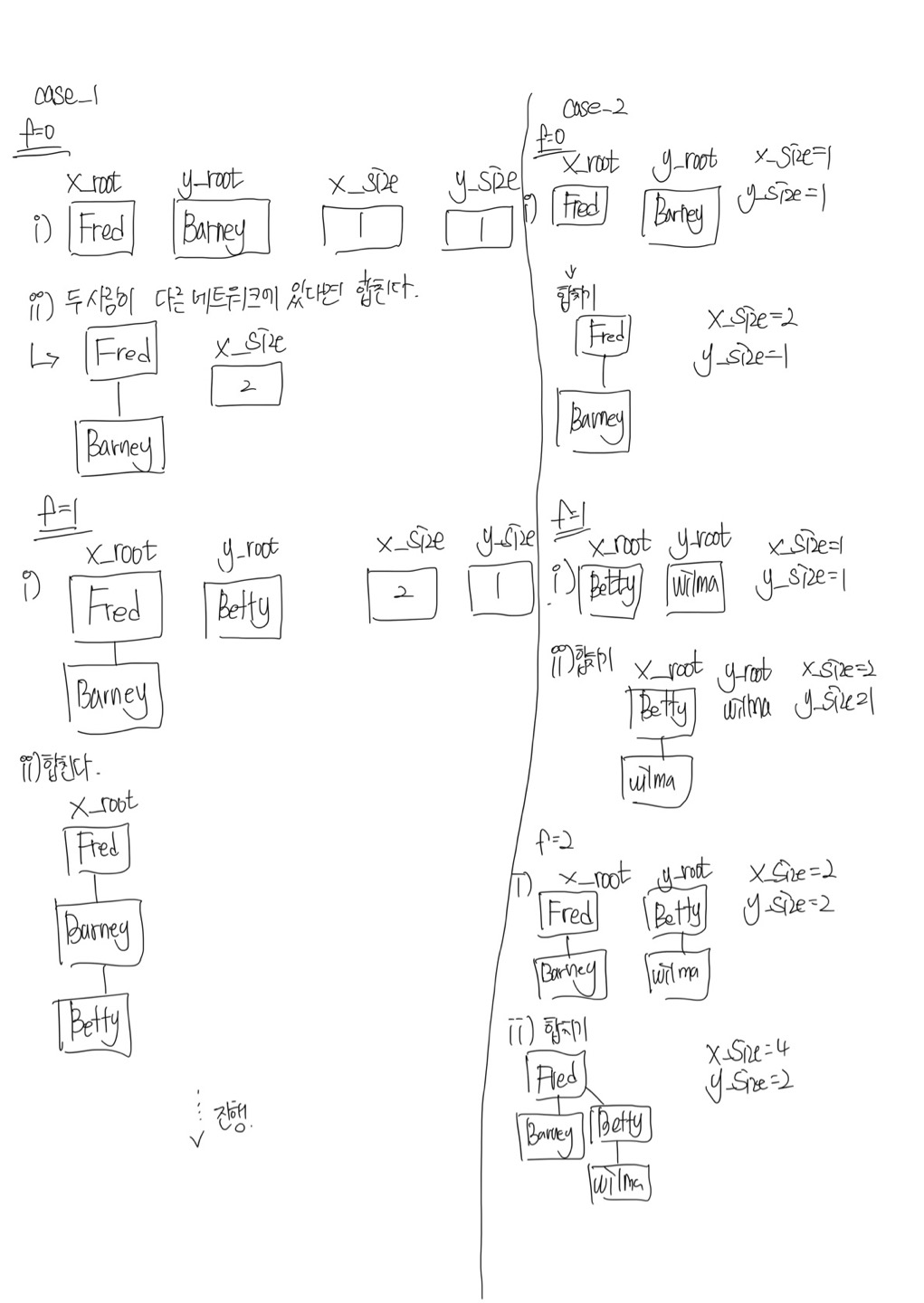
유니온 파인드 알고리즘을 이용한 풀이 입니다.https://newkimjiwon.tistory.com/295
[알고리즘] Union-Find 유니온-파인드(Disjoint Set Union)
Union-Find(또는 Disjoint Set Union, DSU)는 그래프 알고리즘에서 서로소 집합(Disjoint Sets)을 관리하기 위해 사용되는 자료구조입니다. 이 알고리즘은 대표적으로 최소 스패닝 트리(MST) 알고리즘인 Kruskal's
newkimjiwon.tistory.com
'Coding Test > 백준-Python' 카테고리의 다른 글
| 백준 / 두 용액 / 2470번 / Python (0) | 2025.04.09 |
|---|---|
| 백준 / 최소 스패닝 트리 / 1197번 / Python (0) | 2025.04.08 |
| 백준 / 문자열 폭발 / 9935번 / Python (0) | 2025.04.04 |
| 백준 / 부분합 / 1806번 / Python (0) | 2025.04.03 |
| 백준 / 이친수 / 2193번 / Python (0) | 2025.04.01 |

